Je n'imagine pas le discours comme
quelque chose de statique, ni comme
une suite linéaire de mots, ni de phrases, mais comme un
processus qui s'inscrit dans le temps et dans l'espace. Une dynamique,
donc. D'où mon
intérêt pour le déroulement du discours, pour la
disposition et les rapports de forme.
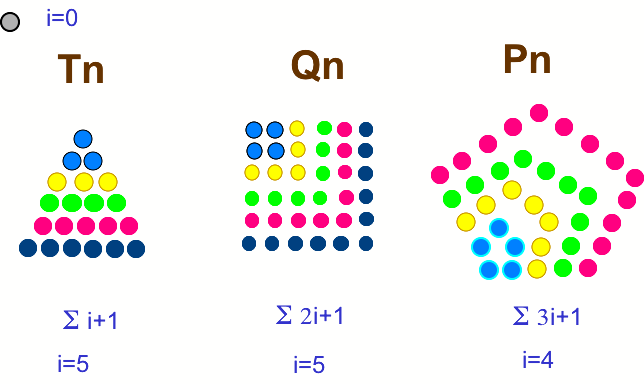
Les quelques
représentations qui suivent expriment des opérations que
l'on peut analogiquement relier à la progression du
récit, à la compréhension, au parcours de lecture.
Elles sont très classiques et tirées de (ou
inspirées par) Nelsen, l'Oulipo, Stevens et Stewart, entre
autres. Mais attention, elles ne représentent pas des textes,
elles ne s'appliquent même pas
directement
à
l'analyse automatique des textes.
Il faut d'abord se donner quelque liberté pour imaginer des
structures (en sciences humaines, une structure est un jeu de
relations). L'activité analytique, les opérations
linguistiques, sont appliquées sur ces structures. Toute la
difficulté dans la transposition du génie linguistique
vers le génie logiciel tient au modèle
d'interprétation, au choix du
référentiel, de l'unité, et
à l'arrondi.
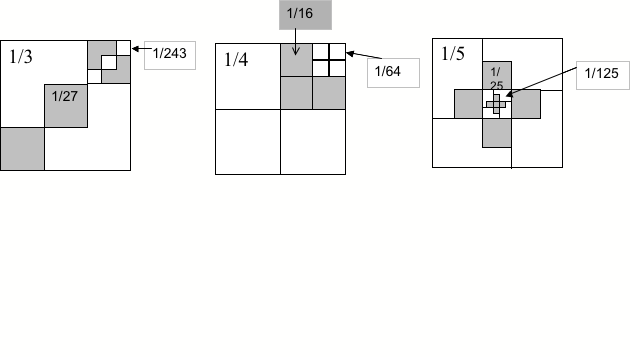
Pour aider à l'abstraction, il y a de belles
formules dans le
vaste champ des mathématiques, qui donnent une idée du
mouvement. Le site
BibM@th est
à voir,
MathWorld
aussi.
